[QLORA] QLORA: Efficient Finetuning of Quantized LLMs

QLoRA

Float vs Int

Float

• Float(부동 소수점) 숫자는 소수점의 위치가 고정 X
• 숫자를 표현하기 위해 가수와 지수로 구성
• 넓은 범위를 표현 가능
• 정수형에 비해 많은 저장 공간 요구

Int

• 정수형 데이터 타입으로 소수점 이하의 수를 포함하지 않는 숫자를 표현
• 저장 공간 적게 사용 가능함
• 표현할 수 있는 값의 범위 더 제한적

IEEE 754 부동 소수점 방식 표현법

부동 소수점 구분: 부호, 지수, 가부

• 부호(Sign): 1비트는 숫자의 부호를 나타냅니다. 0은 양수를, 1은 음수를 의미합니다.
• 지수(Exponent): 8비트는 지수를 나타냅니다. 이는 숫자가 얼마나 크거나 작은지를 결정합니다. 여기서는 Range 그림에 해당
• 가수(Mantissa): 23비트는 가수(또는 유효 숫자)를 나타냅니다. 이는 숫자의 정밀도(정확히 표현할 수 있는 값)를 결정합니다. 여기서는 Precision에 해당

변환 예시

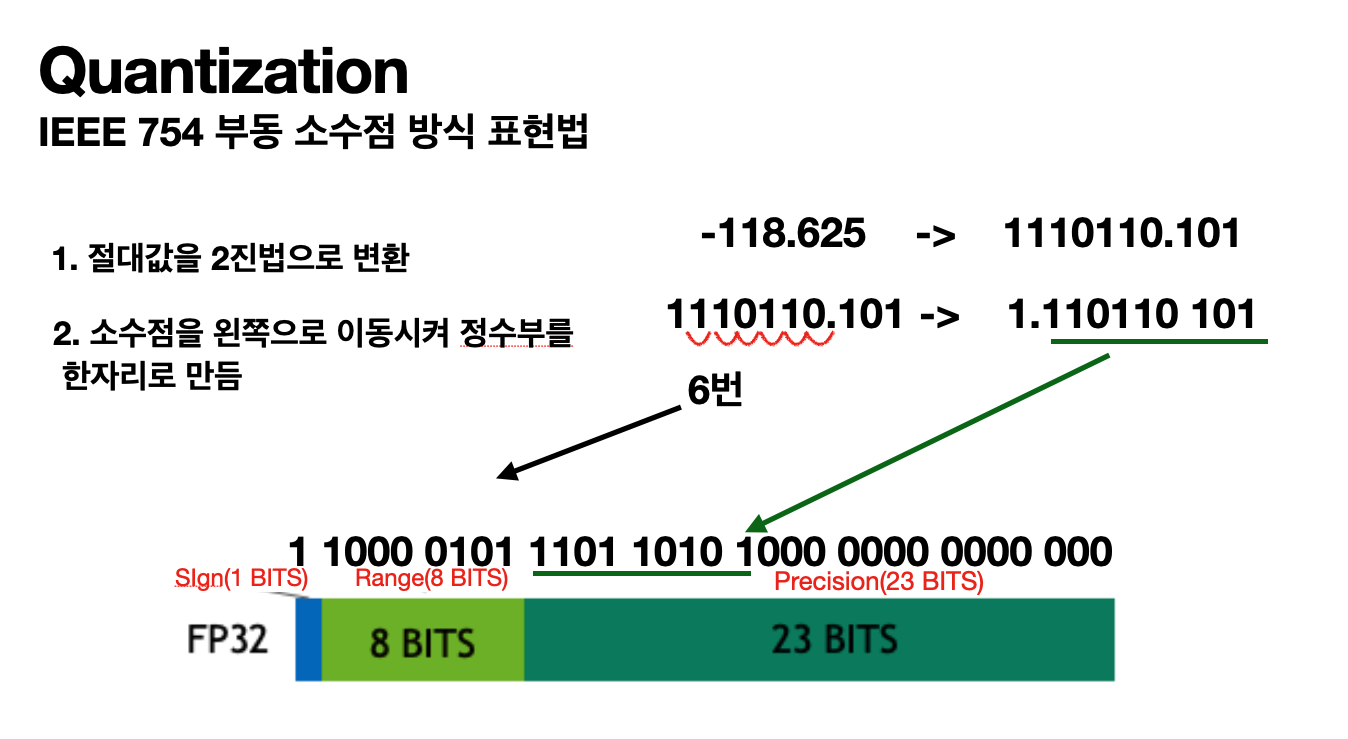
-118.625라는 수를 부동소수점 방식으로 변환

1. 먼저 음수이므로 최상위 최상위 비트를 1로 설정 (양수일 경우 0)
2. 절대값 118.625를 이진법으로 변환 118.625 → 1110 110.101
3. 소수점을 왼쪽으로 이동시켜 정수부가 한자리 되도록 만듬 1110 110.101 → 1.1101 1010 1
4. 3번에서 이동시킨 자릿수(6)만큼을 2의 지수로 사용하여 곱해주고, 이 수를 정규화된 부동 소수점이라고 함 1101 1010 1000 0000 0000 000 x 2^6
5. 32bit IEEE 754 형식엔 "Bias" 라는 고정된 값이 있다 이는 127이며, bias를 2의 지수인 6에 더하고 이진수로 변환  6 + 127 = 133 -> 1000 0101  (8bit 지수부)

Common data types used in Machine Learning

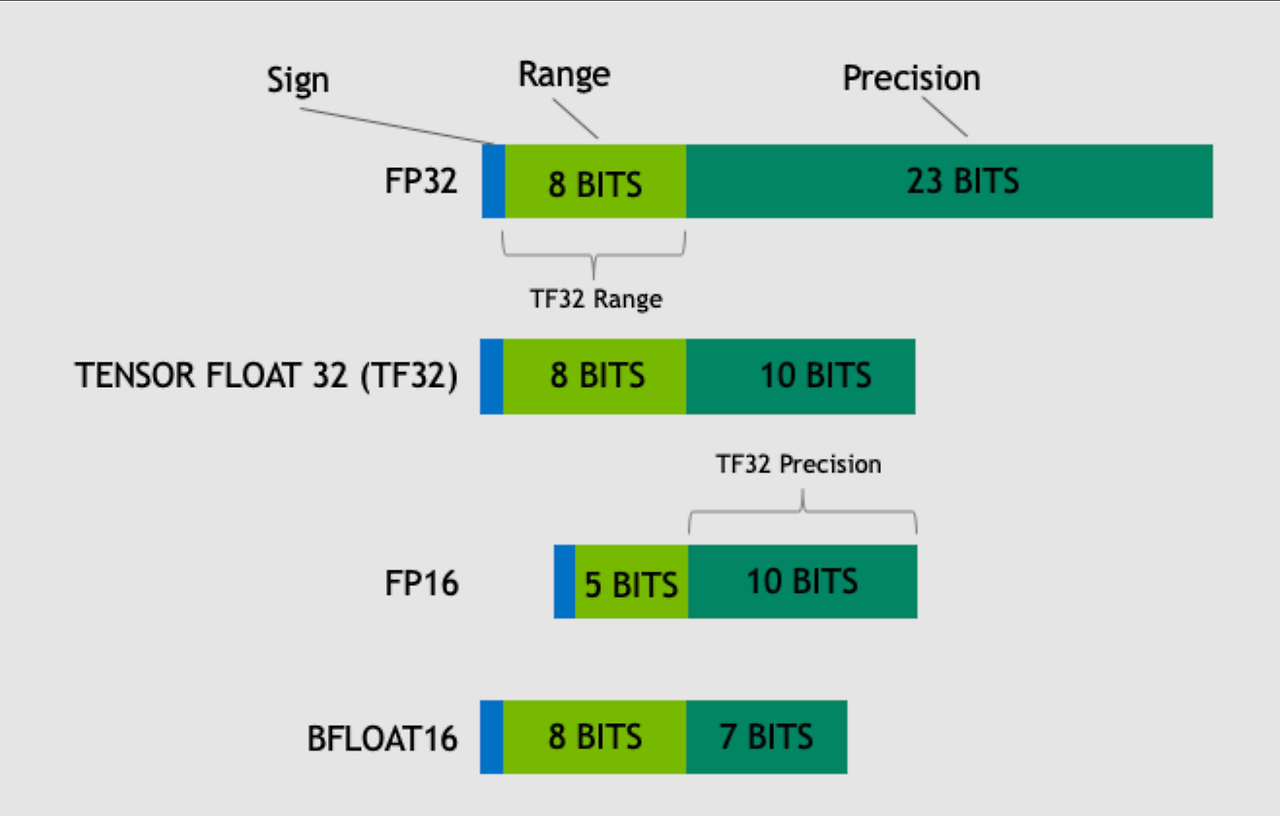
이미지 출처 : nvidia blog

• Float16 (FP16): FP32보다 적은 메모리를 사용하지만, 그만큼 표현할 수 있는 숫자의 범위와 정밀도가 낮습니다.
• BF16 (BFloat16): 지수에 8비트를 사용하여 FP32와 같은 범위의 숫자를 표현할 수 있음, 하지만 Precision(정밀도)가 FP16에 비해서도 낮음

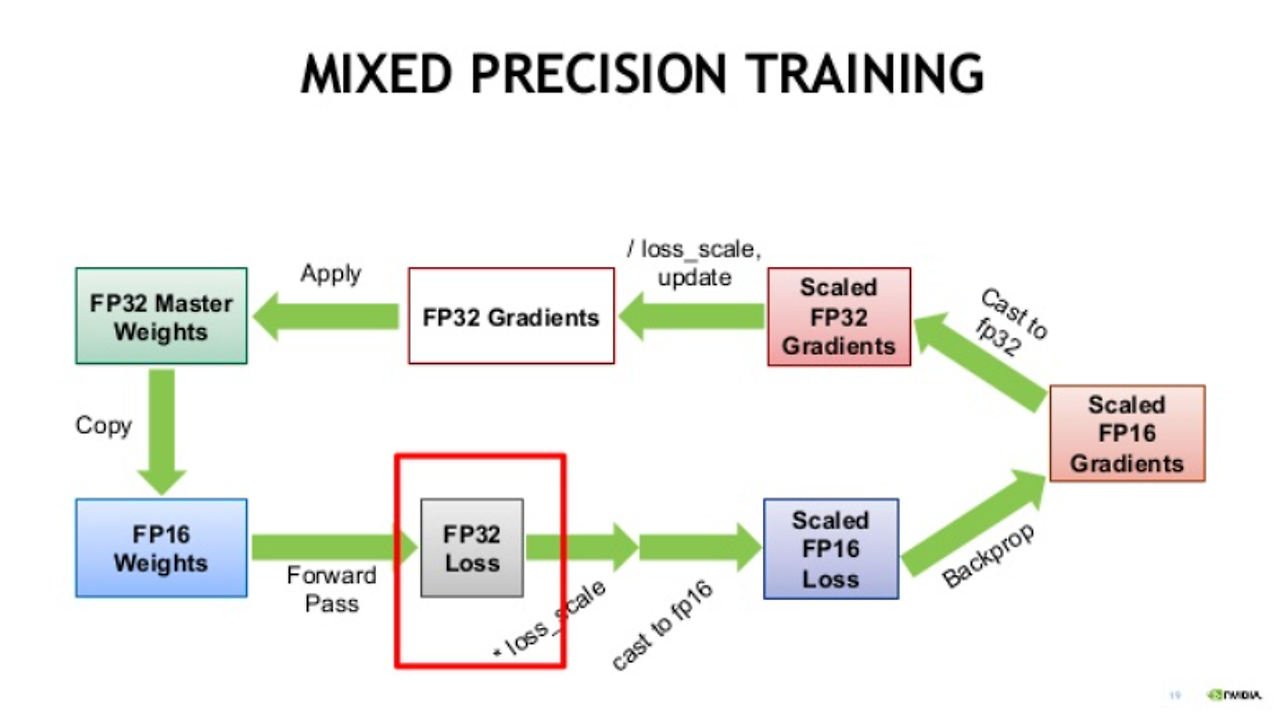
ML에선 FP32를 full precision(4 bytes), BF16와 FP16을 half-precision(2 bytes)라고 부른다. (8bit = 1Byte) 이상적인 학습, 인퍼런스를 위해 FP32가 사용되야 하지만 많은 시간과 자원 소요됨. 그렇기에 mixed precision 방법을 사용한다.

이미지 출처: https://www.slideshare.net/lablup/jmi-techtalk-how-to-use-gpu-for-developing-ai

Quantization

양자화는 모델 가중치와 activation 함수 출력을 더 작은 비트 단위로 표현하도록 변환

8-bit 양자화

• zero-point 양자화 [-1.0,1.0]의 range를 [-127,127]의 range로 양자화 할 때 원본 데이터를 복구하기 위해서는 같은 양자화 수치인 127로 나눔 → 반올림으로 인한 양자화 에러 발생
• absolute maximum 양자화

 

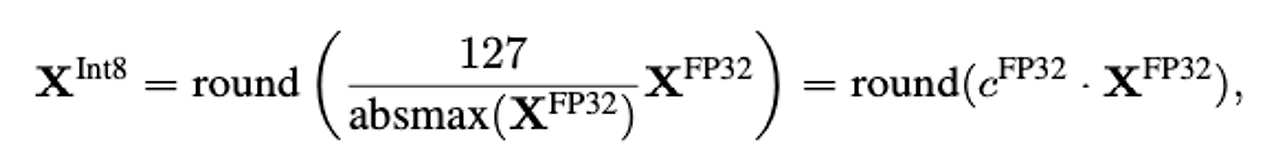
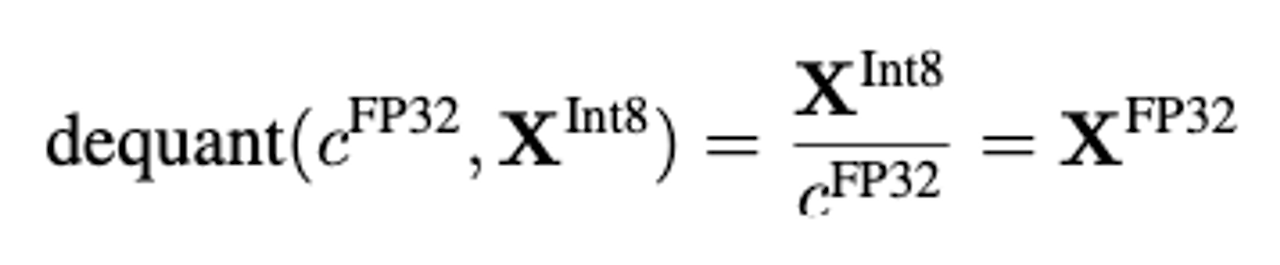
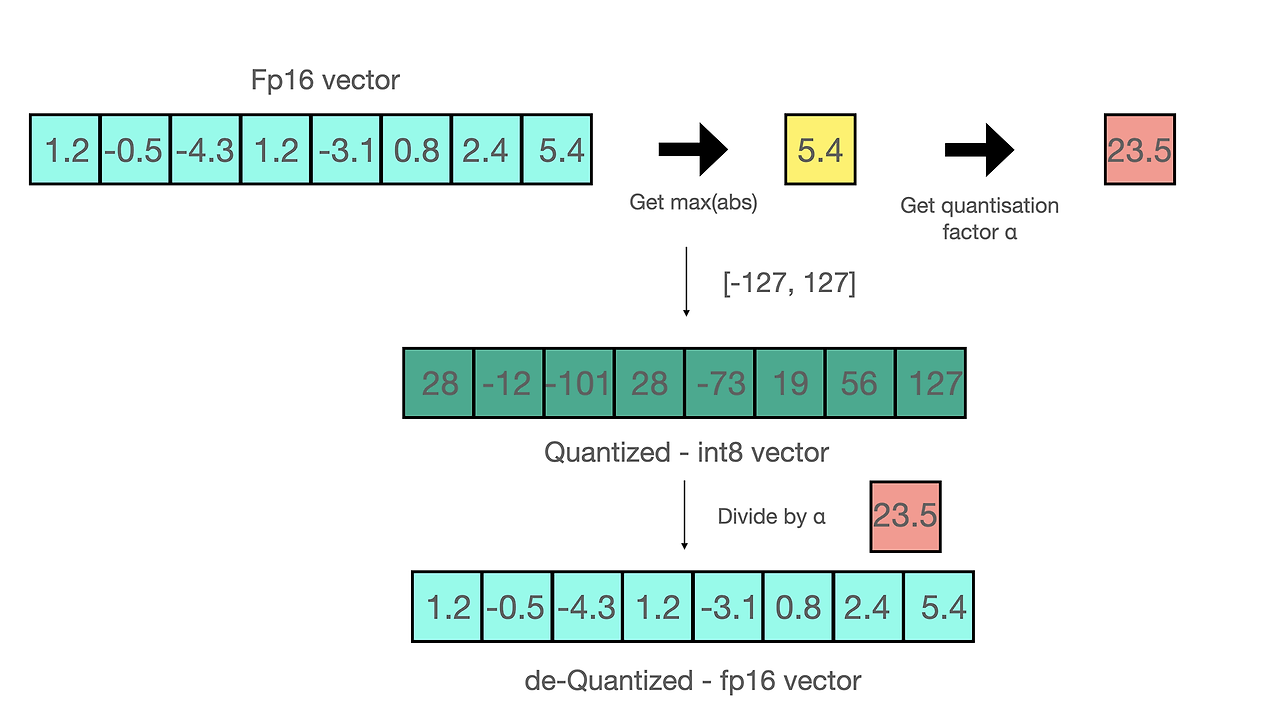
• 양자화의 목적은 모델의 크기를 줄이는 것
• 파라미터를 줄일 수 없기에 precision을 줄여 모델의 크기를 줄이는 것이 양자화이다
• FP32 -> Half precision(BF16, FP16) -> int8의 순으로 연구가 진행
• Half precision의 경우 inference의 성능이 full precision과 비슷하기에 그대로 사용
• half precision을 그냥 반으로 나누어 quater precision(8 bits)를 만들 경우 성능이 드라마틱하게 떨어짐
• absmax 양자화 방식을 사용하여 mapping을 통해 int8 양자화를 진행
• 하지만 여전히 더 경량화 필요

QLoRA Finetuning

 

Block-wise k-bit Quantization

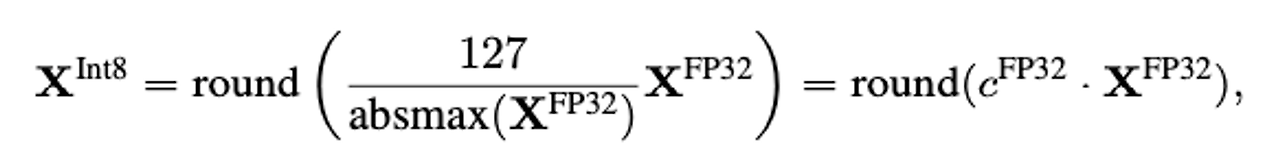
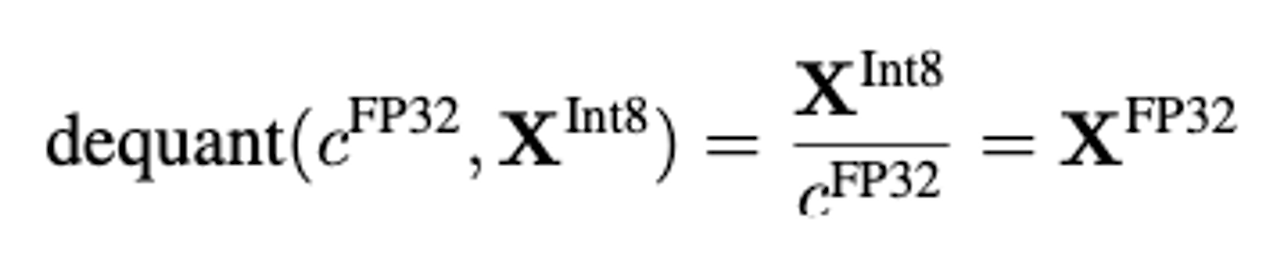
4-bit NormalFloat Quantization (NF4)

Quantile Quantization은 비용이 많이 든다 → SRAM quantiles 알고리즘 → 이것도 근사치의 특성으로 중요한 value에서 large quantization error 발생

이러한 문제는 입력 tensor가 양자화 상수(quantization constant)에 따라 고정된 분포에서 온다면 방지될 수 있다.

pretrained neural network weights는 보통 중심이 0인 정규분포를 따른다.

그러므로 표준편차를 조정해 분포 조정 가능하다.

 

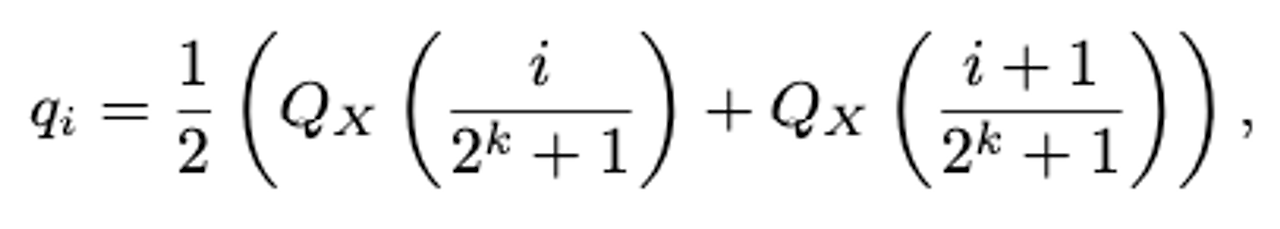
1. quantiles 추정
2. 추정 값의 정규화 얻은 분위수를 사용하여, 정규 분포 값을 [-1,1] 범위로 정규화
3. Input weight tensor 양자화 absolute maximum rescaling을 통해 input weight tensor를 [-1,1]범위로 정규화한다.
4. rescaling된 값을 가까운 NF4로 변환한다.

 다음이 변환된 NF4에 대한 자료이다.

논문에서 제시하는 NF4의 값은 아래 사진과 같다.

Input weight tensor 양자화 과정 예시

 

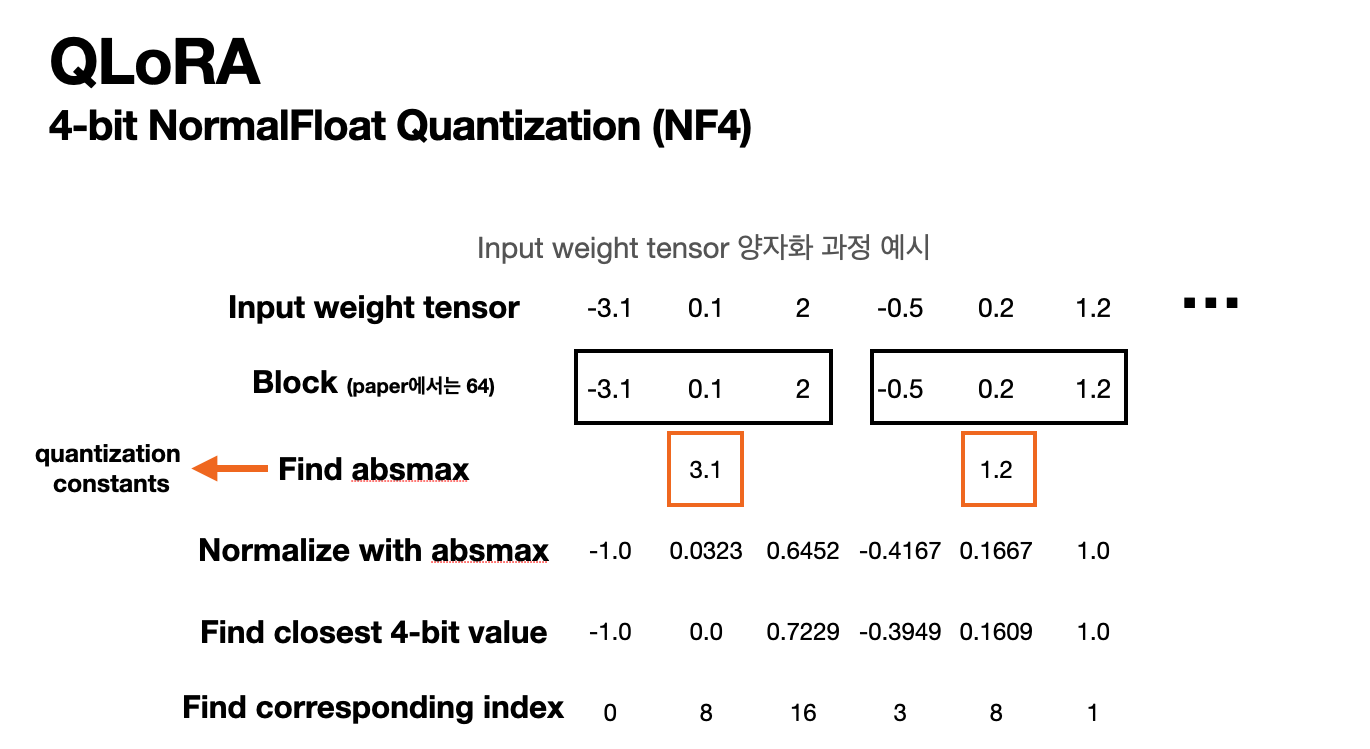
다음과 같은 과정을 통해 양자화가 진행된다. 이때 주황색 박스 안에 있는 숫자 즉, Find absmax의 부분또한 많은 용량을 차지하게 된다. 그렇기에 위 논문에서는 이 양자화 상수(quantization constants)에 대해서 한번 더 양자화를 해준다. 이 과정이 논문에서는 Double Quantization이라고 표현한다.

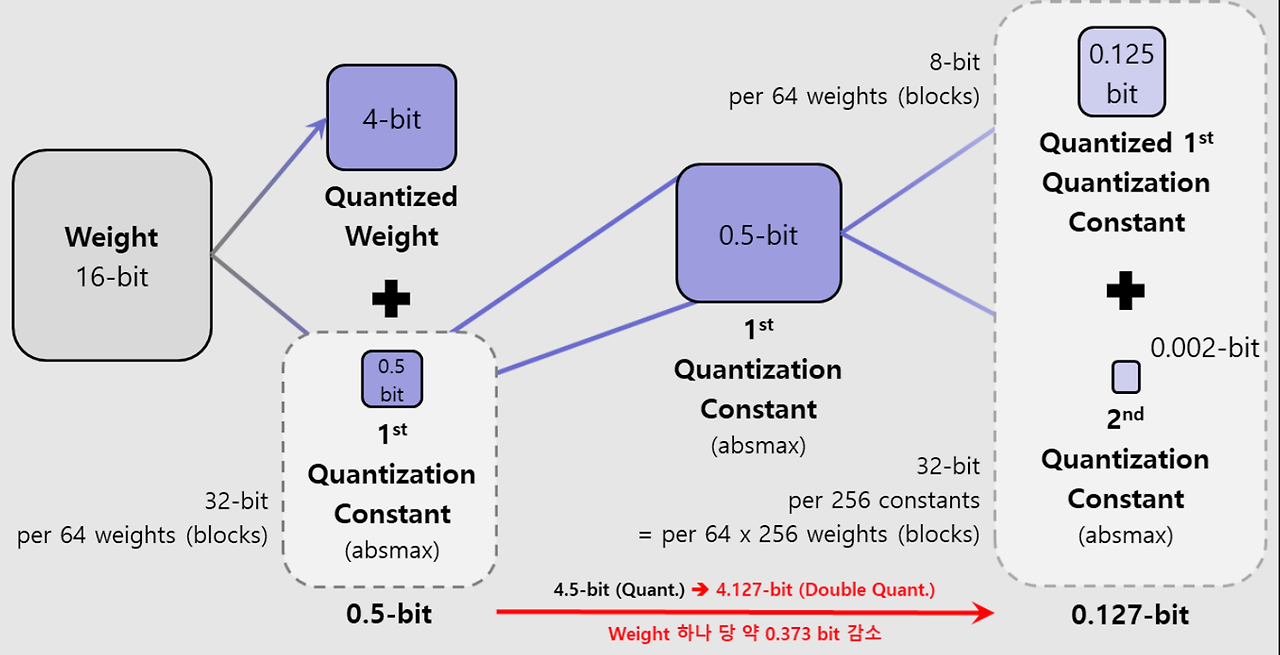
Double Quantization

• 양자화 상수(quantization constants)를 한번 더 양자화 시킴
• 양자화 상수들의 Block size는 256
• 양자화 상수들은 8-bit로 양자화 (8-bit에서도 성능 저하 생기지 않음)
• 양자화 상수 부분의 메모리 절약 가능해짐 0.5bit -> 0.127bit

 

 

 

 

Paged Optimizers

GPU가 가끔 메모리 부족할 때 오류 없는 처리를 위해 CPU와 GPU간에 자동 transfer를 지원

• NVIDIA 통합 메모리 기능
• GPU의 OOM 발생 시, 자동적으로 optimizer state가 CPU RAM으로 이동할 수 있도록 함
• Optimizer의 update step을 위해 GPU에서 optimizer state를 필요로 할 때에는 다시 자동적으로
  GPU로 옮기는 역할

 

QLoRA 수식

 

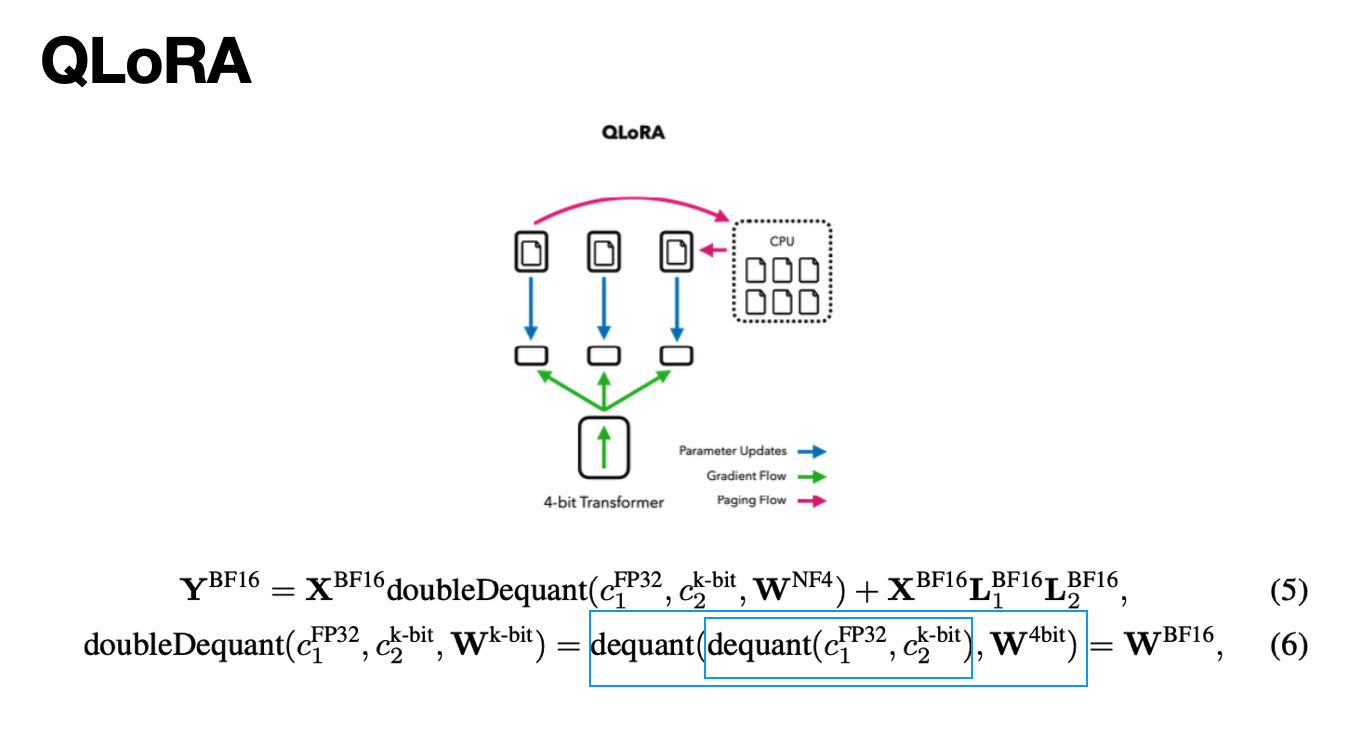
Results

 

 

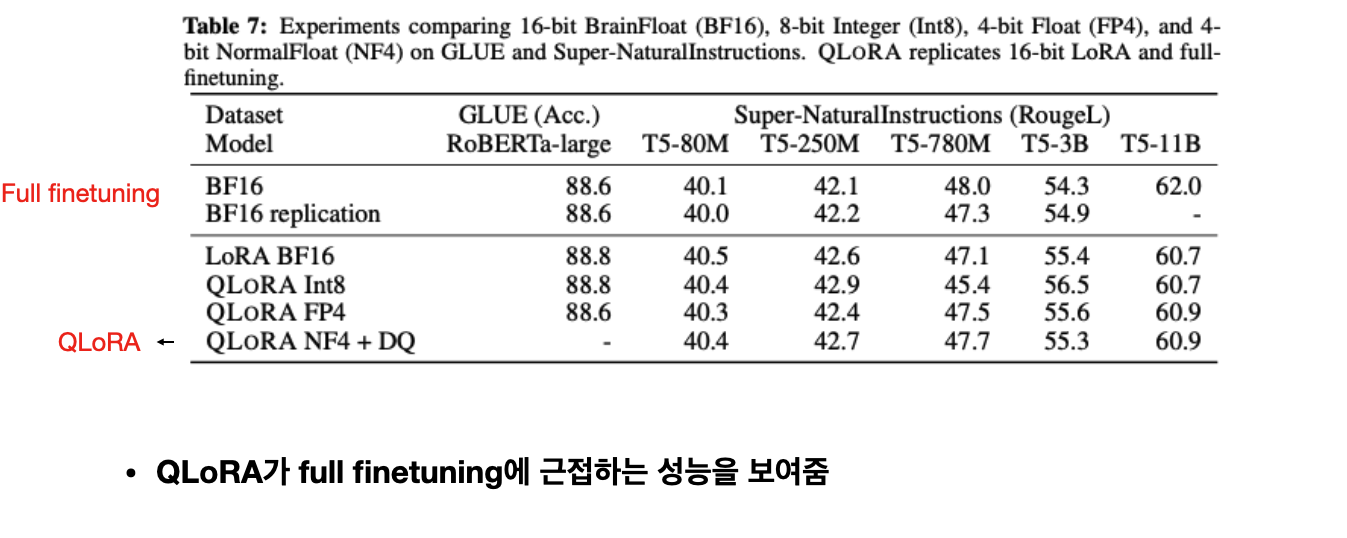
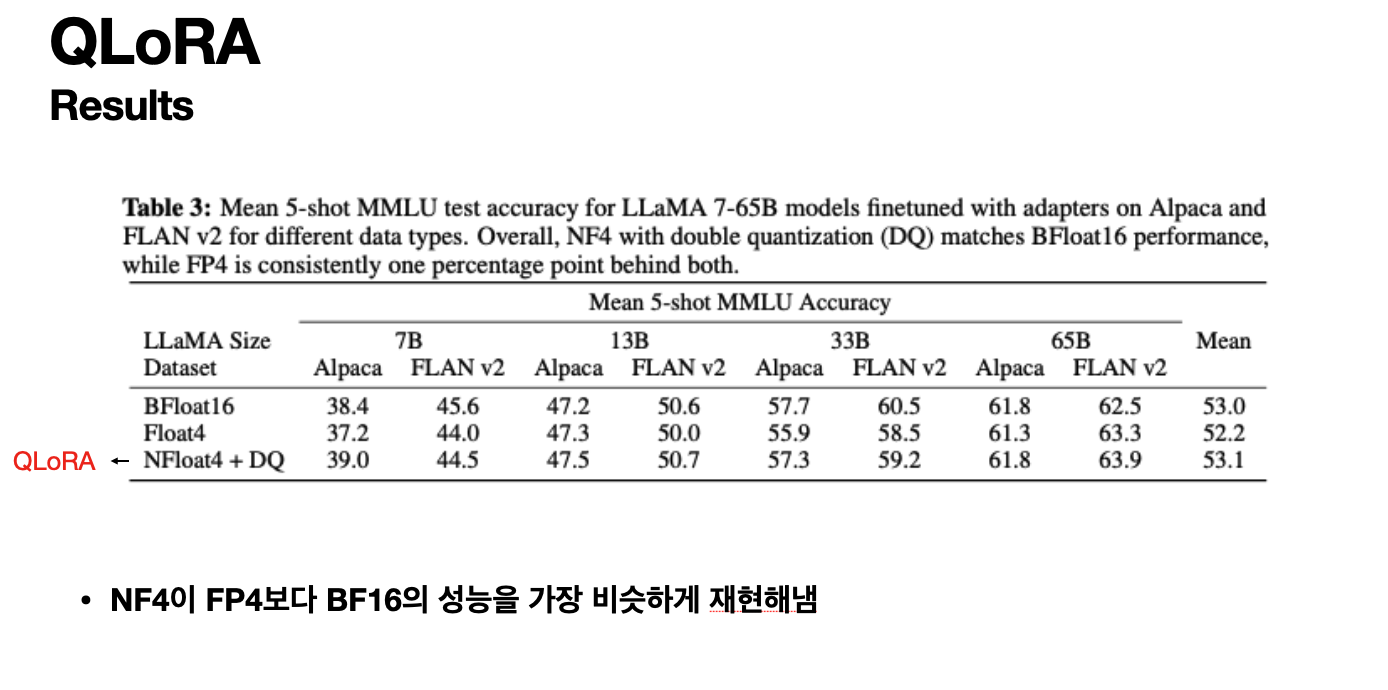
질문!!!!!!!

• 17개로 표현하는게 말이나 되나?
  • 양자화 상수를 이용해서 범위 구분 가능
• 왜 [-1,1]의 범위인가
  • 표준 정규화 해주기 때문에
• 분위수로 양자화를 한다는게 이해 안됨
  • 정규 분포의 구간을 k분위로 나눠 각 분위의 구간마다의 값을 지정
• 양자화를 어떤식으로 하길래 비트가 맞춰지냐 반올림으로 그게 가능하냐?
  • 애초에 4비트에 맞는 NF4를 지정해줌.
• 정규분포를 왜 스케일링하냐 어떤식으로
  • 표준 편차를 1로 만들어 고정된 분포에서의 양자화 값 형성
• absmax는 그냥 스케일링의 역할이냐 양자화랑 다른거냐
  • 그냥 paper에도 적혀있듯이 scaling의 개념이다.